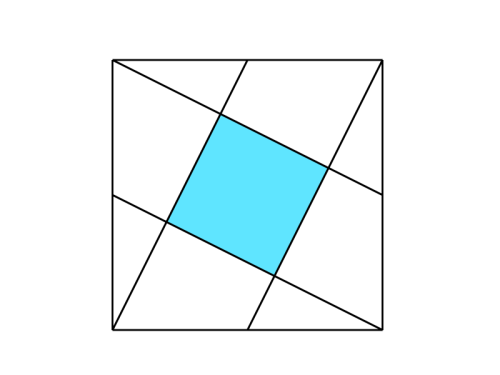
Square in a Square

Tweet

For those of you who don’t wish to read 2000-something words of me pontificating about terrorism, here’s a nice little puzzle:

The large square has a side length of 1. All of the lines within the square begin at the corners and end at the midpoint of an edge. The question is:

What is the area of the light-blue square?

(I realize that many of my maths friends have seen this before, try not to spoil it for everyone else)

I will write the answer and an explanation in the comments in a few days.

(actually, just scroll down for the solution (if you want to see it))

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

keep going

.

.

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution:

so it turns out I can’t post pictures in the comments. So I present the solution here.

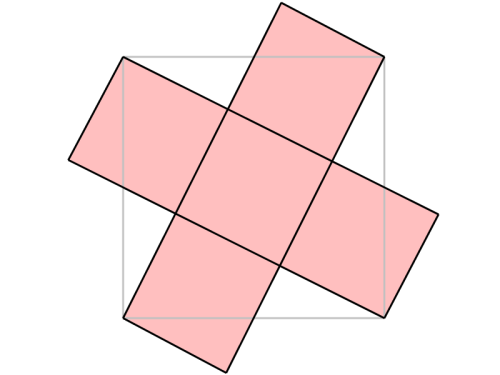
It helps to cut along the lines and try to rearrange things. We can cut out triangles from the original square and then reattach them as illustrated above.

If you repeat several times, you end up with the diagram above – five identical squares with the same area as the original square. So we can safely say that the square in the middle has an area one fifth of the original large square.

Stay tuned for more silly recreational mathematical goodness…