Technical Discussion: The Difference Between Ice and Inline Speed Skating
Aside from the obvious (ice vs asphalt), to the uninitiated, speed skating on ice and inline skates doesn’t look very different. However, to those who have tried either at a competitive level, the differences in technique are more obvious, and to those who have been competitive at both, those differences are substantial. In this article, I will try to examine and determine the root causes for these differences, not only as a recreational, observational exercise, but as this examination may hopefully yield useful information for technique development in both ice and inline skating.
First, we need to establish the basic tenets of skating technique.
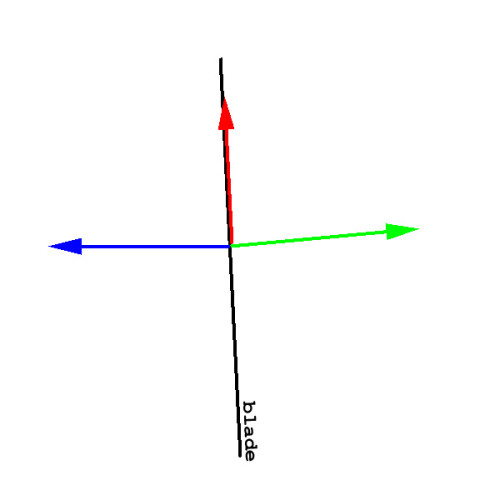
The above diagram is that of a left skate in the straight, viewed from above. The skate points slightly outwards from the center line and force is applied by the skater towards the left, perpendicular to the line of travel (often slightly towards the rear as well) indicated above by the blue arrow. The ground exerts an equal and opposite force in the opposite direction (as per Newton’s third law) but because of the way a skate limits the range of direction of motion (they like to go forwards or backwards along a straight line) it exerts a force back towards the skater (and balancing these forces is what keeps a skater upright when the point of contact with the ground is not directly below a skater’s center of mass). This force is indicated by the green line. These two forces mostly cancel each other out but not quite. Anyone who knows anything about vectors knows that if the blue and the green line aren’t exactly lined up, there will be a third force, indicated by the red line. This is the arrow that drives the skater forwards.
The observant readers will note that if you reduce the angle between the green and blue lines, the red line will be bigger. This can be achieved by turning the skate further away from the center line, and is what happens during the start of a race when the skater is accelerating. The tradeoff is that this kind of pushing cannot be maintained by a very long time because there is a limit to how long a skaters legs can be. The angle has to slowly come closer to being in line with the direction of motion as the skater gets faster.
This is perhaps easier to understand with the above illustration. At the start, the skater is practically running with the skates pointing outwards, and as he gains speed, he has to point his skates more and more forward. Of course, this isn’t the whole story. Skates are designed to be able to turn, and it’s a good thing too because at the high speeds that elite skaters reach, both on the ice and on inlines, even a very slight angle outwards would quickly be unproductive in generating forward force. What eventually happens is the centrifugal/centripetal force generated when a skater turns is used
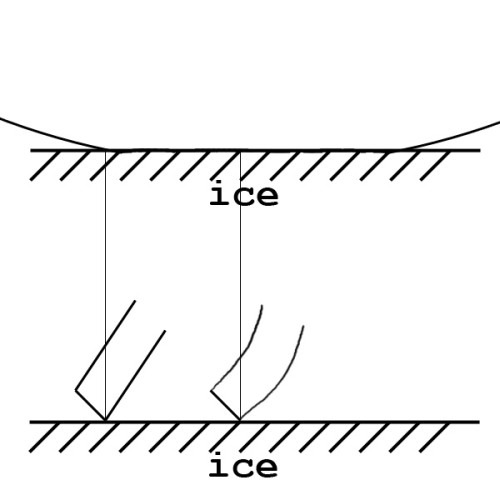
To re-use the convention from a previous diagram, this is how the tracks would look in the ice:
So if these general principles are true for both ice and inline skates, then why the huge difference in technique?
The first major difference in technique is easily explained. Ice skaters are generally lower than inline skaters. On the short track, this is because they experience greater cornering forces (with theoretically infinite grip, compared to the finite grip of inline wheels) so must lower their center of mass just to lean into the corner more effectively. On long track, it is because the speeds experienced are much higher, and the contribution of air resistance to drag is greater. In addition, on the ice there is almost no friction between the blade and the ice, while in the inline world, there is friction and rolling resistance associated with the wheels. This means that not only is air resistance greater on the ice in absolute terms, but it also contributes a much greater percentage to the total resistance a skater must overcome. (that’s why all the world records are set at altitude). I discuss the implications of altitude on skating in more detail here.
For the other differences, I believe it is essential to investigate the interface between skate and skating surface and examine the differences.
As can be seen from the diagrams above, when directly upright, there is little functional diference between an inline wheel and an ice blade. When force is applied on a wheel towards the ground (like when you stand on your skates) the wheel deforms and a larger section of wheel is in contact with the ground, giving you more grip. Putting more force on an ice blade while upright will deform the metal, but much more slightly, almost imperceptibly. It is easy to see how harder wheels would roll for longer than softer wheels, as they would deform less, and less rolling energy would be wasted in changing the shape of the wheel.
Of course, very little time is spent in a completely upright position while one is skating. Usually the blade or wheel is on an angle, or as we skaters call it “edge” (that term probably comes from ice originally, where the “edge” is very obvious and quite sharp).
On the ice, putting the blade at an angle causes it to deform slightly. As it deforms, the contact patch lengthens slightly and also turns into a curved line. On a wheel it deforms (the amount is exaggerated in the diagram). If the wheel is not rotating, this deformation doesn’t change the shape of the contact patch much. However, when the wheels are rotating, it changes the shape of the contact patch so that it “points” in a different direction from straight ahead. This is how inline skates turn.
What are the implications for this? There are a few. Firstly, placing more force straight down on a wheel will make it turn more. This allows a skilled inline skater to generate more force in a straight-push by directing some amount of force straight into the ground. This has the added benefit of increasing the contact patch on the ground, resulting in more grip. This effect is limited with an ice blade simply because the metal doesn’t deform as much as the much softer urethane of an inline wheel. (it also has very different elastic properties).
But there’s more. Consider what happens when more weight is placed on a heel or toe.
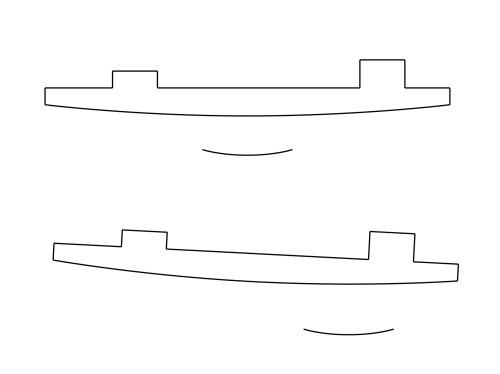
placing more weight on the heel causes the blade to rock back, but the shape of the contact patch is unchanged
weight distributed evenly (top) and more in the heel (bottom), note the differently-shaped contact patches
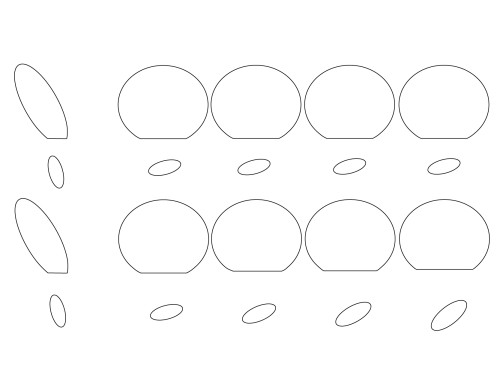
As you can see from the diagrams, rocking back on ice skates doesn’t change the contact patch much (it can change slightly if the blade has a different radius over different sections), however doing the same on inline skates causes the heel to want to steer more than the toe which is a self-correcting behaviour.

perhaps an extreme example, but it shows that inline skaters can be more imprecise with their crossover alignment
This behaviour of the wheels explains many oddities of technique, such as a tendency to “split” the legs (place the left one forward and right one back while both legs are on the ground in the corner) for extra grip on inline skates. It also goes some of the way to explaining why double-push doesn’t work on the ice.1 In a strict technical sense, double push can be made to work on the ice, but the return in speed would be small compared to the extra effort required to execute it properly, and the tradeoff in reduced “normal” push would be too great.

inline straights involve much more twisting and rocking of the hips to maximise the force while the skate is directly under the skater

Ice straights are typified by flat shoulders and hips to maximize the force at the end of the extension (where turning force and grip is greatest)
Biomechanics tells us that generating force in the legs begins at the hips. The hips should be lowest (because lowering the hip gives the leg greater range of motion) during the part of the push where most force is needed. Because of the way wheels deform, and because of the finite nature of grip in the inline world, the most effective part of an inline push happens directly underneath the skater, when the legs are sandwiched between a skater’s center of mass and the ground and is most able to push the wheels into the ground. On the ice, however, where grip is effectively infinite and very little extra benefit is had from pushing an ice blade into the ground, the most effective part of the push happens when a skater’s legs are sandwiched between the skater’s center of mass and the ground at the point when the rotative force is the greatest (to take advantage of the centrifugal/centripetal forces), i.e. when the leg is almost at full extension, and is just beginning to steer back toward the direction of travel (like in the diagram with Joshua Lose and the force arrows).
Corners are much more similar with the main difference being that inline crossovers don’t neet to “cross over” as much (although they work perfectly well if you do them the same as you would on ice). On the ice, because the push is just as effective at the end of the extension as at the start, an ice skaters right hip stays low throughout the movement. On inlines, because there is less leeway to push into the ground near the end of the extension, inline skaters can afford to let their right hips ride a little higher than their left and not loose significant pushing force, and possibly even gain from the easier biomechanics of not having to operate the left hip joint right at the limit of its range of motion. Skating on a banked track (a track where the surface is tilted inwards in the corners) or on a very grippy indoor floor can make this difference less apparent, and good indoor inline skaters often have technique more similar to ice technique.
Footnotes
- “Double Push” is a technique in inline skating where an extra inward push is executed by the skating leg during the early part of the glide phase on the outside edge, before the skate turns over to the inside edge to execute the push. ↩





Very detailed and valuable information, thanks for the effort to explain and share; cheers!
A suggestion:
The diagram with the black blade and the three colored vectors (red, green and blue), disproportionally represents what the red vector’s actual resultant sum size should be. As currently diagrammed, you feed the misconceptions of skaters as to how (@speed) their pushing direction can stay at near 90º yet still effectively increase their momentum. I encounter too many serious veteran skaters who vehemently argue against and dismiss how the actual centripetal acceleration “engine” works, and instead, cling to all kinds of imaginary linear vector diagrams that are supposed to somehow magically 90º-translate the directions of lateral leg push forces into forward rolling momentum surges.
Perhaps you were meaning this diagram to apply to only running at the start, but then the directions do not make sense. Bottom line is that the red vector is a grossly exaggerated in length.
RRLedford@gmail.com