Yeowie’s Technique Lab

Tweet

I once read somewhere that if you took a race-ready rally car, and its street-legal equivalent (say a regular Subaru WRX), swapped the tyres, then drove both of them on a rally course, they would finish with very similar times. Why does this happen? Surely the rally car, with its lighter weight, finely-tuned engine, and suspension would still have enough of an advantage over a run-of-the-mill road car to beat it. Especially in as specialized an event as a dirt rally.

This highlights a point that I keep coming back to in discussions about technique. A car’s tires are its sole interface with the ground. Everything that the car does in relation to making it move has to go through those tires. At a defensive driving course that I did once, the point was made over and over again that putting the best tires that you can afford on your car (and having the correct tire pressure) was the most effective way to make your car safer. And so is the case in running, as well as speed skating that the point at which ALL technical analysis must begin is the point where your foot, or your blade (in the case of speed skating) comes in contact with the ground.

The reason I say this is that, in my new role as a coach, I have had a chance to interact with a lot of other coaches and hear a lot of opinions on things related to elite sports performance. I’ve been an elite athlete long enough to know that very good coaches are extremely rare, although I did expect a slightly higher standard. What I am really trying to say is that I have heard a great deal of nonsense.

Even after a lifetime of experience, no coach can be “perfect”, and that is the rub.

Of course, nobody can or should expect a coach to be “perfect” right out of the box, nor should anyone expect such perfection after many years. Even after a lifetime of experience, no coach can be “perfect”, and that is the rub. An ideal coach’s attitude (as it should be for an athlete) is to always be improving, and to always seek it out. Now if everyone in the world were genetically identical, then it is conceivable that such perfection could be attainable, at least in theory. But people are not identical, conditions are different everywhere, and sports themselves evolve over time.

World records should be evidence enough of this. Take a sport like running – humans have been running for millions of years, our bodies are designed to do it. People have been competing in running races for at least a few thousand years (possibly more), yet world records are still being broken. Why? There are always very small refinements in technique, as well as technology, such as the clothes and shoes that runners wear. There are also constant developments in training methodology, and the pool of eligible athletes is always expanding.

The sum of all those complex parts is a gradual improvement in the overall standard of the sport, and an indicator of that is the fall of world records. So it shouldn’t surprise anyone that it angers me when I hear a coach say something along the lines of “if you want to do this time, then this is what you need to do” where “this” is usually a very specific set of instructions and technique where the athlete is basically a machine simply in need of having certain buttons pressed.

I like to take a more first-principles approach to coaching. Luckily there has been a lot of good research on the subject which allows me to stand on the shoulders of giants. It still surprises me how much the literature obviously isn’t being used by everyone. More esoteric still is the approach to technique.

Running is pretty much the only sport where you can tell an athlete to “just run a lot and what you feel to be the best technique will be it” and expect good results. Even then, most runners can benefit from small adjustments to their running technique, especially sprinters. This is because running is a very natural thing to do, and evolution has tuned our bodies quite well to do it. Just about every other sport must come up with what is necessarily “artificial” technique.

Strangely enough, the history of technique development in most sports indicates that the approach described above for running has been the one applied. Technique development has been a haphazard mix of trial-and-error (mostly error), and chance innovation, usually by sportspeople who train in isolation, or who come from other sports.That doesn’t mean that every sport other than running has rubbish technique, far from it. Those who have innovated have usually been the very best elite athletes, and they have often been very coordinated and possessed good natural biomechanics, which allows them to better feel when their own bodies are acting efficiently or not.

However, many example exist where technique has taken a very sudden leap forward because someone, usually a coach, stopped for a moment and thought about a movement, and how it could be different. The Fosbury Flop is a good example – there’s no way anyone decides that jumping backwards over a pole is a natural way to jump high, but Dick Fosbury realized that the arching of the back allowed a high jumper’s center of mass to be lower than the bar as it was being jumped over. Planting the front foot in a discus throw to get a little extra speed from the “whip” at the end of the spin, and kicking the front foot prior to throwing a javelin in order to take advantage of tendon-tension across the front of the body are two more subtle examples of deliberate technique development which yielded results.

there’s no way anyone decides that jumping backwards over a pole is a natural way to jump high

Not surprisingly now, I turn my attention to speed skating technique. I previously did a preliminary breakdown of skating technique in an attempt to understand the differences between ice and inline skating technique. In that article I concluded that the main reason that differences existed was because of the differences in the way ice blades and inline wheels behave when subjected to changes in force, and changes in angle (relative to the ground).

So you have these points on the ground. Actually they’re curvy lines and they aren’t very big. They provide lateral resistance and are effectively frictionless along their direction of motion. We push against these points in order to move forwards. We begin by simply pushing against them while they’re not moving (i.e. in a standing start), but doing this limits our speed to how fast our muscles can move. Then we start to use the lateral resistance and directional flow, but even this has limitations. Eventually, we use the curve of the blade to generate centrifugal force to give us extra force in our push. This is discussed in a previous post to some extent.

But what are those forces? Perhaps more importantly, what forces are required? Well, anecdotally, since us speedskaters are always being told to feel for “pressure” in the push (that pressure is the angular acceleration perpendicular to the direction of motion of a blade describing a curve on the ice) I will use the most obvious place where we find this “pressure” to come up with a suitable starting number – the corner. The corner radius in a long track is anywhere between 25m and 31m depending on which track you’re skating on, and which lane you’re in. Unsurprisingly, maximum pressure is found in a corner of the smallest radius, so we’ll take 25m.

Next we need some speed. The fastest skaters can skate a lap of a 400m oval in about 24 seconds, which comes to 60km/h or m/s. The cornering force that the skater must overcome is given by:

a skater skating a 24 second lap would be pulling 1.13 ‘g’s around the inner corner

This gives F to be 11.1ish (actually ) multiplied by the skater’s mass in kilograms. Just to give you a sense of scale for these forces, the force of gravity is about 9.8N per Kg of mass, so a skater skating a 24 second lap would be pulling 1.13 ‘g’s around the inner corner. Just for reference, you have to skate a 25.55 second lap to be pulling exactly 1g. This is significant because the lean you need to get in a corner to overcome a 1g cornering force is exactly 45 degrees.

 

As you can see, 45 degrees is actually quite a steep lean, and a 24 second lap would require even more. Just how much more is a matter of  remembering our sine and cosine rules.

Why is determining the angle important? Because it allows us to calculate the forces acting on the skater. We already have the force of gravity (9.8N) and and the centrifugal force (11.1N), but as you can see from the diagram, a skater doesn’t push directly down, or directly to the outside of the corner. A skater necessarily pushes along a line from the point of the center of mass to the point where the blade comes into contact with the ice, and this is where that angle becomes important. For the 25.55 second lap, when the cornering force and the force of gravity are equal (and the angle is 45 degrees) we simply add and which is about 13.86N per kilogram of bodyweight. When we go a little faster  we have to add and which comes to 14.52N per kilogram of bodyweight.

In other words, that extra 1.55 seconds of speed is worth just short of one extra newton of cornering force per kilogram of bodyweight. If you weigh 70kg, then that’s the difference between 970.2 newtons (the equivalent of lifting 100kg) of cornering force and 1016.4 newtons (the equivalent of lifting 104kg). Not forgetting, of course, that you’re doing this “lifting” with one leg while balanced on a sliver of metal 1.1mm thick, and travelling at 60km an hour. I’m sure anyone who’s ever done a 1-rep max test can tell you how much difference just a few kilograms can make when you’re right on the limit.

don’t forget that you’re doing this “lifting” with one leg while balanced on a sliver of metal 1.1mm thick, and travelling at 60km an hour

Of course, this is not the whole story, it is only the starting point. This is only a force requirement. Ultimately, we would like to calculate the “work” requirement (force distance), and the “power” requirement (the rate of work, or more precisely ). If you’ve been paying attention, you will realize that the force requirement says nothing about movement (which is, sadly, a rather inescapable element of speed skating). I weigh 72kg, so 14.52N per kilogram of bodymass is equivalent to the force that a 107kg weight would exert on me. I’m pretty sure I can’t do a 107kg one-legged-squat, but if I stand up straight, I can probably hold much more weight. Of course, if I skated with my legs straight, or close to it, I wouldn’t go very fast because there are other forces to overcome than cornering forces.

There is also air resistance. I covered this aspect of the sport briefly in this post, mostly to highlight what I perceived to be incorrect decisions regarding selection, which were impacted by not taking into account the importance of the altitude at which times were skated. In short, altitude makes a difference to air resistance, and air resistance is such a significant factor in speed skating (some say as high as 80%) that even small difference in air resistance can have a measurable impact on times. In that previous post, I introduced this equation:

is the force, is the air density is velocity is area is drag coefficient and is a direction vector for the velocity. Using some fairly simple mathematics, I was able to show that going from sea level to 1400m (the elevation of the Utah Olympic Oval) reduces aerodynamic drag by about 15%. I say “simple” because at no point did I actually have to calculate the force, I only needed to calculate the difference between two forces. But now that we are trying to calculate force requirements, it is time to get our hands dirty.

Let us begin at a typical indoor oval at sea level with favourable conditions of about 5 degrees ambient temperature. The air density would be 1.269kg per cubic meter. For velocity, we’ll take our 24 second lap (60km/h), for frontal area I’ve ripped off some approximate numbers from journal articles that variously discuss skiers and cyclists who have gone through the trouble of wind tunnel testing. For frontal area, I’m using 0.45 square meters, and for drag coefficient I’m going to use 0.6. When you plug all these numbers into the formula you get 47.59N. That may not seem like much, but when you consider that it is the force required simply to stay at a constant speed, it is significant. Look at it another way, in a frictionless vacuum, 47.59N of constant force would push a 72kg mass (me) in a straight line to 60km/h in just over 25 seconds and do it in just over 200m.

Which brings me nicely to my final point of this post (which seems to have ballooned out into something much bigger than I anticipated). The force required for a skater to actually accelerate. Without exception, all individual skating distances begin with a standing start. So far this analysis has only looked at the forces required to maintain a speed of roughly 60km/h (which is certainly at the high end of what is currently possible in the skating world). Getting there is another matter entirely.

all skating distances begin with a standing start – this analysis has only looked at forces required to maintain speed – getting there is another matter entirely

When calculating the acceleration required, we encounter a strange dilemma. The very best sprinters in the world can skate a standing 100m in about 9.5 seconds. We’ll round up to 10. Assuming constant acceleration over that 10 seconds (which would carry the requirement of the least amount of force), a skater would have to accelerate at 2 meters per second, per second (i.e. at the end of the first second, they would be traveling at 2m/s, at the end of the second second, the would be traveling at 4m/s etc.) This gives exactly 10 seconds for 100m, and the force required to achieve this is exactly 2m (so for a 72kg mass, a force of 144N is required (which is the same force as a 14.7kg mass exerts due to gravity). This doesn’t seem like such a big deal until you realize that acceleration isn’t constant because, for reasons explained above and in previous articles, there are technical limitations. Also, a 2 meter per second per second constant acceleration leaves you traveling at 20 meters per second (72km/h), well above the top speed of any skater.

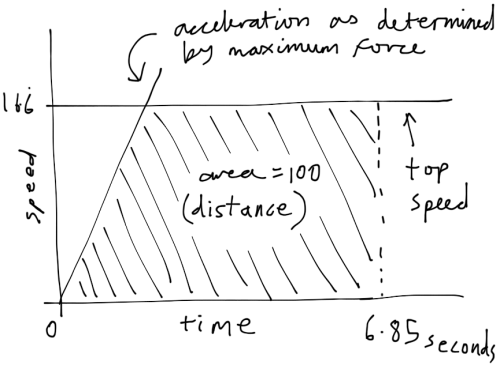
Luckily, we have an easy way out of this. We know that our 60km/h-capable skater can exert a force of 14.52N per kg of body mass which is the same as saying that our skater apply force to accelerate at 14.52 meters per second per second which can take us up to 16.6 meters per second in well under two seconds, and since you only have to travel at 16 meters per second for 6.25 seconds to cover 100m, we have easily solved our original dilemma, and are now left with the question of why standing 100m splits are so slow, given that fast skaters can apply so much force. After all, if you can accelerate at 14.52 meters per second per second, it takes you 1.15 seconds to reach 60km/h. Assuming this is your top speed, you would only have to skate at this speed for another 5.7 seconds to cover 100m – that’s a standing 100m in 6.85 seconds!

Obviously the curves are much smoother, and the fact that force isn’t the only variable to consider comes into play. Remember that our figure of 14.52 is the force required to keep everything in balance at a certain speed, as soon as your body moves, the numbers will be different because there are physical limitations to the rate of work you can do (power), and even if there weren’t there are physical limitations to how fast you can move parts of your body.

Ultimately, the answer lies in biomechanics, which I hope to cover in a later post.