Mid-Life Calculation

Posted on Tuesday, June 14, 2011 by in Blog, Science // 2 Comments

It is a fairly well-known truism that time seems to pass at a slower rate for children than it does for adults. One day, not long ago, I was pondering the unusual behaviour of a seven-year-old who had just been reunited with his mother after having been away for only two weeks. Two weeks doesn’t seem like a lot to me, after all for a 29-year-old, it represents a measly \frac{1}{750} of one’s life experience. However to a 7-year-old, it represents \frac{1}{175} of one’s life experience. To put that into perspective, two weeks to a 7-year-old would seem like just over two months for a 29-year old.

This thought spawned a little dinner table discussion with some friends and the question was put to the table “if our perception of time decreases like this, then when are you truly half way?”. Well, obviously if one takes the average age to be, say 80 years, then halfway wouldn’t be at 40, but at some point before then, but when? This spawned a simple but interesting back-of-the-envelope (actually, it was scribbled on my new ipad) calculation with a slightly counterintuitive result.

We begin at the beginning. Your first day/week/month/year of your life represents 100% of your life experience, and your second represents a half, and so on. One quickly realizes that we are forming a harmonic series.

1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\ldots

So we have a few results already, because of what we know about the harmonic series. First, we know that, even though the individual terms converge to zero, the sum does not converge at all. So the sum of your perceived life experience doesn’t converge to a number, but really does depend on how long you live for (which, frankly, is a relief). From this, it is an easy deduction that the halfway point in this “perceived experience measure” also depends on the length of life we select for our calculations, and it must be finite.

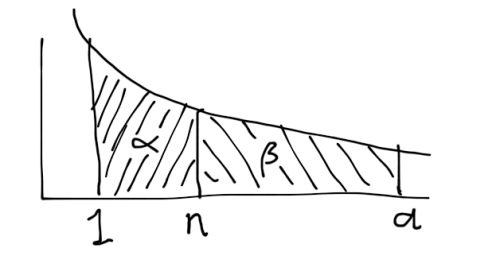
So we have the graph of \frac{1}{x} which should be familiar to anyone who has passed high school maths. We need to find the area under the graph between 1 and some number a(the life expectancy age) to determine the total “experience”, then we divide that number by 2 and find some number n(the perceived-life-experience halfway point) for which the area under the graph between 1 and n is that number. So first:

\int_{1}^{a} \frac{1}{x} dx

which just turns out to be \log_e{a}. Half of that is simply \frac{\log_e{a}}{2}. So all we have to do is rearrange the equation:

\log_e{n} = \frac{\log_e{a}}{2}

so…

\frac{\log_e{n}}{\log_e{a}}=\frac{1}{2}

\log_a{n} = \frac{1}{2}

n = a^{\frac{1}{2}}

n=\sqrt{a}

Which is not what you expect… In fact, I almost put an exclamation mark at the end of that result, except in mathematics, that would have an actual meaning (factorial). So this basically means that if you expect to live to a hundred, then your “percieved life experience” halfway point is actually when you’re 10, which is considerably lower than 50. So much so that I keep thinking that I have the wrong result.

Obviously, this doesn’t account at all for the fact that we tend to forget things that happened when we were very young, and recent memories are slightly stronger and so on, but even so (assuming that I haven’t made a mistake in my working) this is an interesting result.

I’d like to hear people’s thoughts on this…

Related Articles:

  1. Population Paradox

  2. It changed my life

  3. A Week in the Life

  4. Signs of Life

  5. Undo the Folded Lie

  6. Letters From… Malta

2 Comments on Mid-Life Calculation

  1. Barr // Wednesday, June 15, 2011 at 12:13 // Reply

    I have a couple of objections with the posit, but since this is designed to be a light-hearted look I’ll restrict it to the obvious one: first memory. For the average person, the first memory is much later than 1 year, so your start choice is poor. Once you put in a first memory of f, you’ll find that the mid-life crisis occurs at n = sqrt(f*a). To put this in perspective (depending on source), if your first memory is at 3 1/2 years, and you’re expected to live to 80, then your mid-life crisis occurs at sqrt(280) ~ 17 years… pretty much when you were a rebellious teenager, as pretty much as expected.

  2. bartogian // Sunday, June 19, 2011 at 2:52 // Reply

    Taking sqrt{a} is not dimensionally consistent. eg if a=100 yrs then sqrt{a}=10 sqrt{yrs} which is not a length of time. So by dimensional analysis reasons one should stand up and scream that the purported answer can’t be a good model. (Barr’s formula passes the dimensional consistency test at least).

    ps. let’s drop the subscript e from the logs and unite against the oppressors that teach the log symbol as defaulting to base 10.

Leave a comment

Your email address will not be published.


*