Population Paradox

Tweet

Let’s say you’re a government minister, and you’ve been tasked with the job of controlling the population. There’s one catch – in the country where you live, it is very culturally important to have a male child. Simply limiting family size to two children results in families risking having two daughters which may lead to illegal births or, at worst, infanticide. What do you do?

You sweat over this for a few weeks until one of your interns suggests a solution to you while spilling your coffee on the photocopier. She suggests that you allow every female of the population to continue having children until they have a male child. Once they’ve given birth to a male child, then they are required by law to stop.

You ponder this for a while. Obviously, allowing everyone to have a male child will be very popular with the electorate, but can we really simply allow everyone to keep trying until they get one? Surely this would result in some kind of population explosion. Worse yet, wouldn’t it result in some kind of huge imbalance in the male-female ratio?

Actually no. The ratio remains at exactly 1:1, and the birth rate is exactly 2 – zero growth.

The mathematics is not particularly difficult. One can easily write out a table of all the probabilities and the required figures (the birth rate and the gender ratio) can be found by way of summing infinite geometric series. But how are you going to convince the electorate of this rather counter-intuitive result?¹

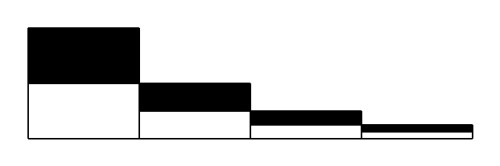
Let’s start by drawing a box.

This box represents the first child. Let’s say it’s of unit-size, representing one child. I’ve coloured half of the box black and the other half white indicating that the probability that the child is a boy is one half, and the probability that the child is a girl is also a half.

Of course, if the child is a girl, we get to try again. That box should only be a half the width of the original because there’s only a half the chance that the event it represents will happen. The length of the box should still be one though, because given that it does happen, it still represents one child. The colour scheme is identical to the first box. We can repeat this as many times as we want, but I will stop at four.

What this is really representing, is that the probability of having exactly one boy is a half, the probability of having exactly one girl and one boy is a quarter, the probability of having exactly two girls and one boy is an eighth, and so on. The diagram however, allows you to very easily see why the gender ratio stays exactly balanced – when you sum all the probabilities, you’re still going to get the same ratio of boys to girls. In fact, using the rule suggested by the intern will preserve a gender ratio reflective of the probability of having a boy or a girl, which we have assumed to be 50:50.

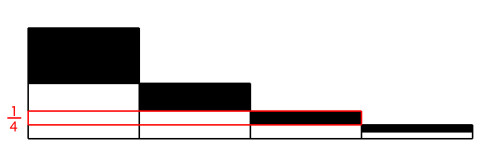
The question of population growth is slightly more tricky. Below is the same diagram, except with one of the cases highlighted.

We could think through every single one of these cases and add them up. And it’s not even a very difficult thing to do. But if you’re a government minister, you’re probably too lazy even for that. So what about…

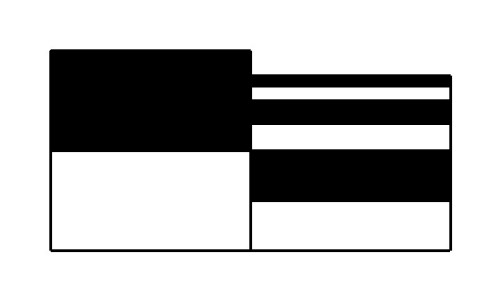
All I’ve done is stack the boxes differently. If we continue stacking the progressively smaller boxes on top of each other, you will get a gap of etc., until you eventually end up with a gap at the top of which equals zero (in an asymptotic sense) and voila! You have a box that is one by two, giving your expected value of births per mother to be two.

This is a good way to control overpopulation because the birth rate should be about 2.1 for a steady population (because not all babies will live long enough to reproduce) and 2 is significantly lower than 2.1. (Things like twins don’t have much of an effect, as they only account for 2% of live births)

Just quietly, I don’t believe that implementing a policy like this would be an easy thing to do. Despite the obviousness of the mathematics, there is no doubt in my mind that many will cry foul and drum up all manner of absurd conspiracy theories accusing the government of taking away freedom and the like. That, of course, will all be a smoke screen for the real problem which is, despite the public school system, not too many people appreciate the absolute truth of mathematics, and will sooner accept a better-sounding and more intuitive dogma, handed down by a loud radio show host, than actually bother to listen to reason.