The Earth Debate: Part 2

In part 1 of The Earth Debate, it was established that warming was taking place, and that the consequences of warming were not good for humans. I wanted to get those points out of the way first because they are the easiest, and are widely accepted as fact, even by most so-called climate change skeptics. The response so far has been fairly quiet, with no real objections raised, but merely more questionable material from the skeptic’s camp being brought to my attention.
There are generally two main things which are wrong with arguments coming from skeptics and they are as follows: bad argument structure, and bad science. Argument structure is really something that we should all be able to spot, although sometimes this is difficult, especially if the idiot skeptic is a good writer. Bad science is even more difficult for the layperson to spot because it is difficult for a person without formal training in the field of climate science to tell, becuase they lack the requisite background knowledge. In this part, I will attempt to give some of this background knowledge in the form of explanation of ![]() and the greenhouse effect, which will hopefully provide the link between human activity (
and the greenhouse effect, which will hopefully provide the link between human activity (![]() emissions) and the warming of the Earth.
emissions) and the warming of the Earth.
WARNING: The following contains mathematical equations. Don’t be discouraged, if you are, for whatever reason, afraid of mathematical equations (and who isn’t a little bit afraid), then feel free to skip over them. It should not significantly detract from the learning experience.
First, an obvious statement – we get all our energy from the Sun. There are actually minor exceptions, like nuclear power and geothermal power, but the vast majority of all the energy we deal with came from the Sun at some point. The effective temperature of the sun is just short of 6000 Kelvin. The radiation from the sun spreads out according to the inverse-square law and a tiny fraction of it hits the Earth. The Earth reflects some of this radiation, and the radiation that is absorbed is eventually re-emitted. This happens because the energy coming in must be the same as the energy going out (otherwise the Earth would get hotter and hotter, or cooler and cooler).
Planck’s law tells us about the distribution of the wavelength emitted by a blackbody. This is important because it tells us how much of each wavelength is emitted by the Earth. Certain gases in the atmosphere absorb (and subsequently re-emit) radiation at different wavelengths. First, let’s look at the emissive curves of the Earth and the Sun.
(note the logarithmic scales and poor resolution)
The crucial thing to take away from this, is that the peak emissions wavelength for the Earth is mostly in the infrared while the Sun’s is just past the visual and towards the ultraviolet. This translates to the fact that most of the energy coming in to the Earth is coming in at a different wavelength to that going out.
So we need to calculate the energy flow coming from the surface of the Earth. Turns out that there is this law called the Stefan-Boltzmann law which states that this radiative flux is directly proportional to the fourth power of the temperature. The equation is very simple, it looks like this: flux![]() . (
. (![]() is the Stefan-Boltzmann constant, and is about
is the Stefan-Boltzmann constant, and is about ![]() ).
).
So… it seems we have enough to figure out what average temperature the Earth ought to be. Turns out, with this information alone, we get a figure of about 254 Kelvin, or -18 Celsius, which clearly isn’t true. (If you’re interested, the equation is ![]() where S is the solar flux – 1360
where S is the solar flux – 1360 ![]() , and A is the albedo (the reflective index of the Earth) which is about 0.3, I shall leave the derivation of this to the interested reader). Some of you may have already guessed the omission from our calculations is the atmosphere.
, and A is the albedo (the reflective index of the Earth) which is about 0.3, I shall leave the derivation of this to the interested reader). Some of you may have already guessed the omission from our calculations is the atmosphere.
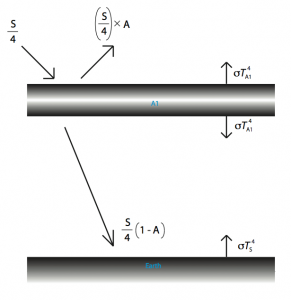
What the atmosphere basically does, for the sake of our calculation, is absorb outgoing radiation, then re-radiate it. How can this possibly make a difference? Well, the outgoing radiation is coming from one direction while the re-radiated energy goes in all directions, some of it coming back to the Earth. Why doesn’t incoming radiation also get absorbed? You may ask. This is because the wavelengths at which incoming radiation comes in are different from those of the outgoing radiation. Most gases have what’s called an absorption profile which is a fancy way of saying that it will absorb energy at certain wavelengths while at other wavelengths, it will be effectively invisible. I have illustrated what is happening in the diagram below.
The temperature is simply: ![]() . To find
. To find ![]() we use
we use ![]() and
and ![]() , and a simple substitution yields a temperature at the surface of 302.7 Kelvin which is about 30 degrees Celsius.
, and a simple substitution yields a temperature at the surface of 302.7 Kelvin which is about 30 degrees Celsius.
There are two major greenhouse gases in the atmosphere, and they are ![]() and
and ![]() .
. ![]() , due to the water cycle is self-regulating and the amount of it at any one time in the atmosphere doesn’t change a great deal.
, due to the water cycle is self-regulating and the amount of it at any one time in the atmosphere doesn’t change a great deal. ![]() , on the other hand, stays in the atmosphere for years and the processes for taking it out and putting it into the atmosphere are very slow, that is until humans came along.
, on the other hand, stays in the atmosphere for years and the processes for taking it out and putting it into the atmosphere are very slow, that is until humans came along.
no, that is not a typo, we are PAST the safe level
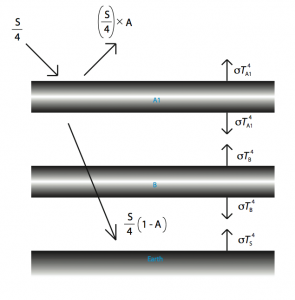
So, pre-industrial ![]() levels were about 270 parts per million (ppm), and at the moment, they are at about 385 ppm. FYI scientists believe that the maximum “safe” level is about 350 ppm (no, that is not a typo, we are PAST the safe level). For simplicity’s sake, let’s double the amount of greenhouse gases in the atmosphere, and see what happens. In terms of our diagram, it is equivalent to adding another “slab” of atmosphere.
levels were about 270 parts per million (ppm), and at the moment, they are at about 385 ppm. FYI scientists believe that the maximum “safe” level is about 350 ppm (no, that is not a typo, we are PAST the safe level). For simplicity’s sake, let’s double the amount of greenhouse gases in the atmosphere, and see what happens. In terms of our diagram, it is equivalent to adding another “slab” of atmosphere.
Intuitively, it looks like it will get warmer, but just how much warmer?
Our first equation – the one whose solution we are interested in, would look like this: ![]() . But to find the value of
. But to find the value of ![]() , we will need
, we will need ![]() and
and ![]() . These equations might look very scary, but the substitutions are, in fact, very simple (and to think I got extra credit on an assignment for doing this).
. These equations might look very scary, but the substitutions are, in fact, very simple (and to think I got extra credit on an assignment for doing this). ![]() comes to about 335 Kelvin, or 62 degrees Celsius, which is alarmingly high.
comes to about 335 Kelvin, or 62 degrees Celsius, which is alarmingly high.
Obviously, this isn’t true, because, as I mentioned before, ![]() is one of many greenhouse gases and is the second most important one behind
is one of many greenhouse gases and is the second most important one behind ![]() (because there’s a bit more
(because there’s a bit more ![]() in the atmosphere). But the point is made that adding more
in the atmosphere). But the point is made that adding more ![]() is going to shift the temperature equilibrium of the planet towards a warmer state.
is going to shift the temperature equilibrium of the planet towards a warmer state.
The trouble with a lot of the critics of the theory of anthropogenic climate change, is that they get so caught up in the politics and the back-and-forth that inevitably goes on in research (which most of these pundits hardly understand) that they miss some of the very basic science that underpins these theories. Obviously, this is not the whole story, but this is the most important part of it. This is the distilled essence of the answer to the question of “how is ![]() linked to warmer temperatures?”. So the next time someone tells you that they heard somewhere that there is no link between CO2 and climate change, you can tell them that they’re full of shit, and point them in the direction of this page.
linked to warmer temperatures?”. So the next time someone tells you that they heard somewhere that there is no link between CO2 and climate change, you can tell them that they’re full of shit, and point them in the direction of this page.
In part 3: Oceans, feedback, and other reasons that increased CO2 is bad
Don’t forget to check out the other articles in the Earth Debate series.


Leave a comment